Паралельність площин: ознака, умова

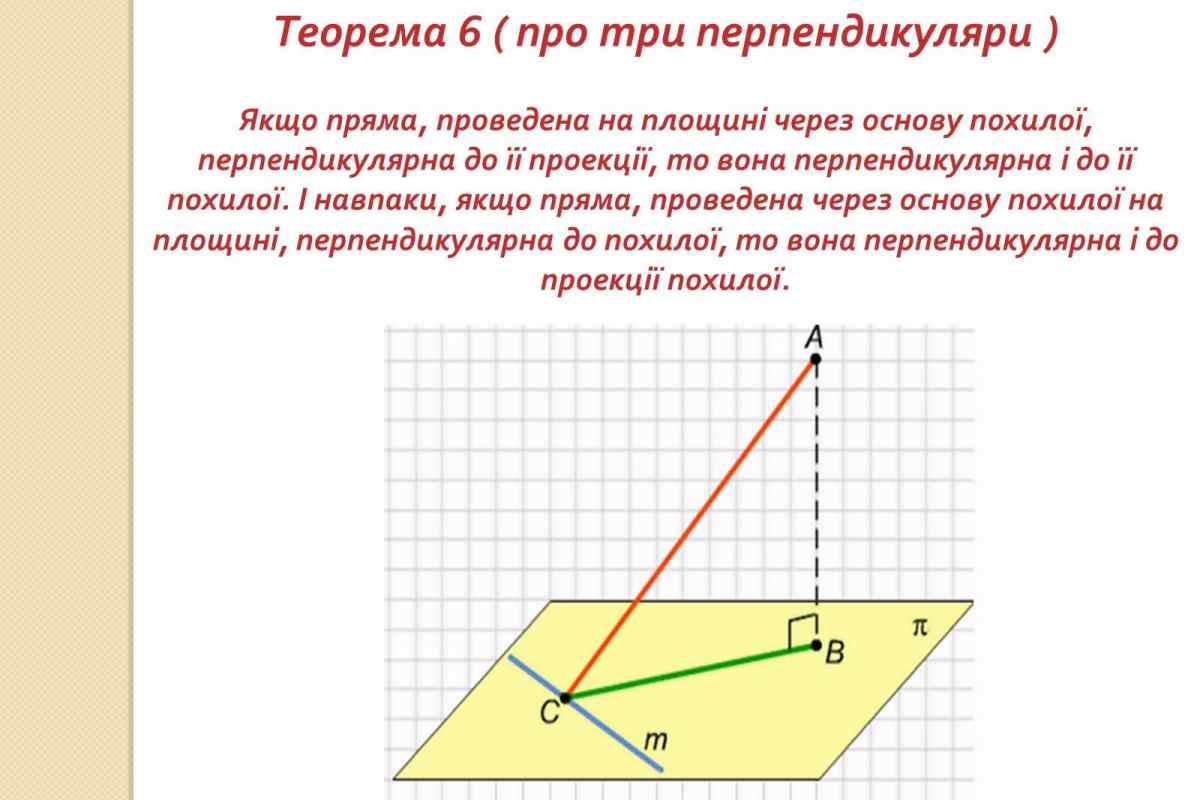
Всім, хто коли-небудь навчався або зараз навчається в школі, доводилося стикатися з різними труднощами при вивченні дисциплін, які включені в програму, розроблену Міністерством освіти.

З якими труднощами доводиться стикатися

Вивчення мов супроводжується зазубренням наявних граматичних правил і основних винятків з них. Фізкультура вимагає від учнів великої викладки, хорошої фізичної форми і величезного терпіння.

Однак ні з чим не можна порівняти ті складнощі, які виникають при вивченні точних дисциплін. Алгебра, що містить заплутані способи вирішення елементарних завдань. Фізика з багатим набором формул фізичних законів. Геометрія та її розділи, в основі яких лежать складні теореми та аксіоми.

Прикладом можуть служити аксіоми, що пояснюють теорію паралельності площин, які необхідно обов 'язково запам' ятати, оскільки вони лежать в основі всього курсу шкільної програми зі стереометрії. Давайте спробуємо розібратися, як простіше і швидше це можна зробити.

Паралельні площини на прикладах

Аксіома, що вказує на паралельність площин, звучить наступним чином: "Будь-які дві площини вважаються паралельними тільки в тому випадку, якщо вони не містять загальних точок", тобто не перетинаються один з одним. Щоб більш детально уявити собі дану картину, в якості елементарного прикладу можна навести відношення стелі і статі або протилежних стін в будівлі. Стає відразу зрозуміло, що мається на увазі, а також підтверджується той факт, що ці площини в звичайному випадку ніколи не перетнуться.

Іншим прикладом може служити віконний склопакет, де в якості площин виступають полотна скла. Вони також ні за яких умов не будуть утворювати точок перетину між собою. Додатково до цього можна додати книжкові полиці, кубик Рубіка, де площинами є його протилежні грані, та інші елементи побуту.

Позначаються розглянуті площини спеціальним знаком у вигляді двох прямих "||", які наочно ілюструють паралельність площин. Таким чином, застосовуючи реальні приклади, можна сформувати більш чітке сприйняття теми, а, отже, можна переходити далі до розгляду більш складних понять.

Де і як застосовується теорія паралельних площин

При вивченні шкільного курсу геометрії учням доводиться стикатися з різнобічними завданнями, де часто необхідно визначити паралельність прямих, прямої і площини між собою або залежність площин один від одного. Аналізуючи наявну умову, кожну задачу можна співвіднести до чотирьох основних класів стереометрії.

До першого класу відносять завдання, в умові яких необхідно визначити паралельність прямої і площини між собою. Її рішення зводиться до доказу однойменної теореми. Для цього потрібно визначити, чи є для прямої, не належної розглянутої площини, паралельна пряма, що лежить в цій площині.

До другого класу завдань належать ті, в яких задіюють ознаку паралельності площин. Його застосовують для того, щоб спростити процес доказу, тим самим значно скорочуючи час на пошук рішення.

Наступний клас охоплює спектр завдань щодо відповідності прямих основних властивостей паралельності площин. Вирішення завдань четвертого класу полягає у визначенні, чи виконується умова паралельності площин. Знаючи, як саме відбувається доказ того чи іншого завдання, учням стає простіше орієнтуватися при застосуванні наявного арсеналу геометричних аксіом.

Таким чином, завдання, умова яких вимагає визначити і довести паралельність прямих, прямої і площини або двох площин між собою, зводяться до правильного підбору теореми і рішення відповідно до наявного набору правил.

Про паралельність прямої і площини

Паралельність прямої і площини - особлива тема в стереометрії, оскільки саме вона є базовим поняттям, на яке спираються всі наступні властивості паралельності геометричних фігур.

Згідно з наявними аксіомами, у разі коли дві точки прямої належать деякій площині, можна зробити висновок, що ця пряма також лежить у ній. У сформованій ситуації стає ясно, що можливі три варіанти розташування прямої відносно площини в просторі:

1. Пряма належить площині.
2. Для прямої і площини є одна загальна точка перетину.
3. Для прямої та площини точки перетину відсутні.

Нас, зокрема, цікавить останній варіант, коли відсутні будь-які точки перетину. Тільки тоді можна говорити про те, що пряма і площина відносно один одного є паралельними. Таким чином, підтверджується умова основної теореми про ознаку паралельності прямої і площини, яка свідчить, що: "Якщо пряма, яка не належить розглянутої площини, паралельна будь-якій прямій на цій площині, то розглянута пряма також є паралельною даній площині".

Необхідність використання ознаки паралельності

Ознака паралельності площин, як правило, використовується для пошуку спрощеного вирішення завдань про площини. Суть цієї ознаки полягає в наступному: "Якщо є дві прямі, що перетинаються, що лежать в одній площині, паралельні двом прямим, що належить іншій площині, то такі площини можна назвати паралельними".

Додаткові теореми

Крім використання ознаки, що доводить паралельність площин, на практиці можна зустрітися із застосуванням двох інших додаткових теорем. Перша представлена в такій формі: "Якщо одна з двох паралельних площин паралельна третій, то і друга площина або теж паралельна третій, або повністю збігається з нею".

Базуючись на використанні поданих теорем, завжди можна довести паралельність площин щодо розглянутого простору. Друга теорема відображає залежність площин від перпендикулярної прямої і має вигляд: "Якщо дві невпадаючі площини перпендикулярні по відношенню до деякої прямої, то вони вважаються паралельними один одному".

Поняття необхідної та достатньої умови

При неодноразовому вирішенні завдань докази паралельності площин було виведено необхідну і достатню умову паралельності площин. Відомо, що будь-яка площина задається параметричним рівнянням виду: А1х + В1у + C1z + D1 = 0. Наша умова базується на використанні системи рівнянь, що задають розташування площин в просторі, і представлена наступним формулюванням: "Для доведення паралельності двох площин необхідно і достатньо, щоб система рівнянь, що описують ці площини, була несумісною, тобто не мала рішення".

Основні властивості

Однак при вирішенні геометричних завдань використання ознаки паралельності не завжди буває достатньо. Іноді виникає ситуація, коли необхідно довести паралельність двох і більше прямих в різних площинах або рівність відрізків, укладених на цих прямих. Для цього застосовують властивості паралельності площин. У геометрії їх налічується всього два.

Перша властивість дозволяє судити про паралельність прямих у певних площинах і представлена в наступному вигляді: "Якщо дві паралельні площини перетнути третьою, то прямі, утворені лініями перетину, будуть також паралельні один одному".

Сенс другої властивості полягає в тому, щоб довести рівність відрізків, розташованих на паралельних прямих. Його трактування представлене нижче. "Якщо розглядати дві паралельні площини і укласти між ними область, то можна стверджувати, що довжина утворених цією областю відрізків буде однакова".