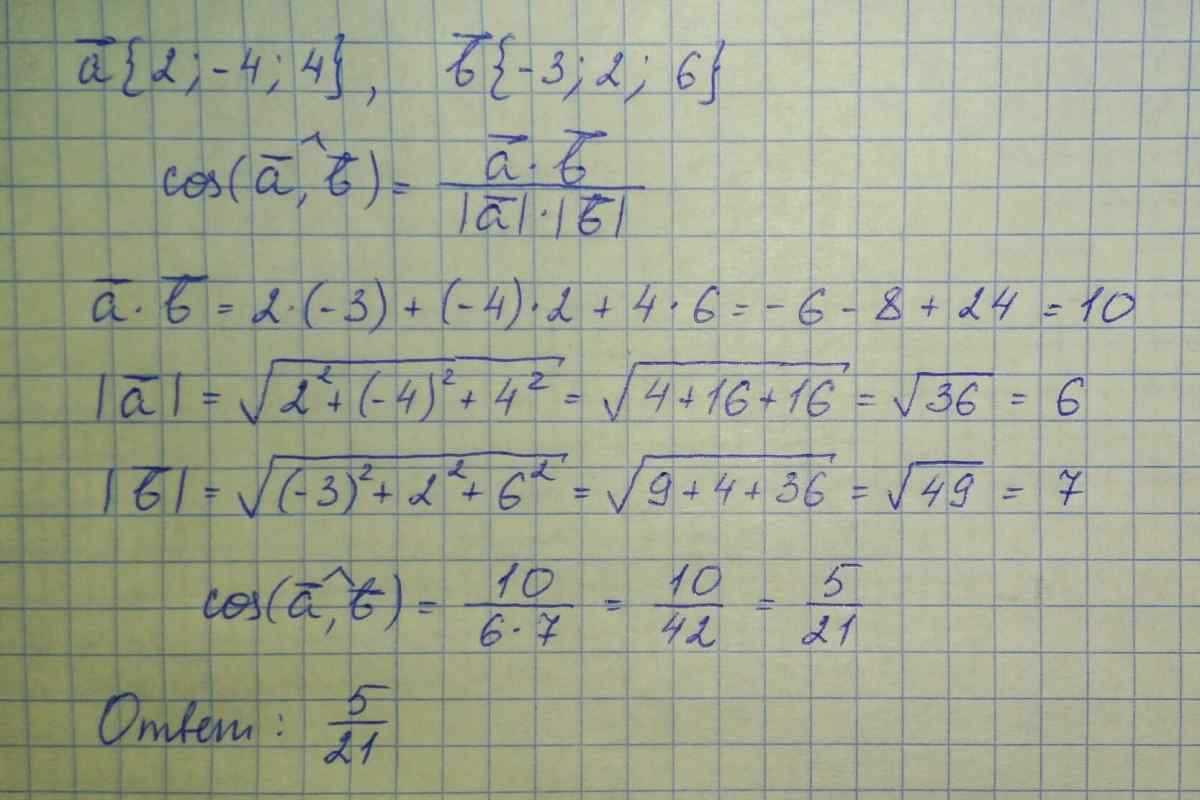Для вирішення багатьох завдань, як прикладних, так і теоретичних, у фізиці та лінійній алгебрі необхідно обчислювати кут між векторами. Це просте на перший погляд завдання здатне доставити безліч труднощів, якщо ви чітко не засвоїте сутність скалярного твору і яка величина з 'являється в результаті цього твору.
Інструкція
1. Кут між векторами в векторному лінійному просторі - мінімальний кут при повороті, на який досягається сонаправленість векторів. Обертається один з векторів навколо його початкової точки. З визначення стає очевидно, що значення кута не може перевищувати 180 градусів (див. малюнок до кроку).
2. При цьому абсолютно справедливо передбачається, що в лінійному просторі при здійсненні паралельного перенесення векторів кут між ними не змінюється. Тому для аналітичного розрахунку кута просторова орієнтація векторів не має значення.
3. Коли ви знаходите кут, використовуйте визначення скалярного твору для векторів. Дана операція позначається наступним чином (див. малюнок до кроку).
4. Результат скалярного твору - число, інакше скаляр. Запам 'ятайте (це важливо знати), щоб не допустити в подальших розрахунках помилок. Формула скалярного твору, розташованого на площині або в просторі векторів, має вигляд (див. малюнок до кроку).
5. Цей вираз справедливий тільки для ненульових векторів. Виберіть кут між векторами (див.
6. Якщо система координат, в якій розташовуються вектори, є декартовою, вираз для визначення кута можна переписати в наступному вигляді (див. малюнок до кроку).
7. Якщо вектори розташовуються в просторі, розрахунок робіть аналогічним способом. Єдиною відмінністю буде поява третього доданого в ділимому - це доданок відповідає за аплікату, тобто третю компоненту вектора. Відповідно, під час обчислення додатка векторів компоненту z також необхідно врахувати, тоді для векторів, розташованих у просторі, останній вираз перетворюється таким чином (див. малюнок 6 до кроку).