Ще зі шкільної програми з алгебри та геометрії нам відомо, що вектором називається відрізок, що має напрямок. Координати вектора визначають його характеристику і є впорядкованим набором чисел. Знайти їх абсолютно нескладно, згадавши деякі відомості зі шкільного курсу навчання.
Інструкція
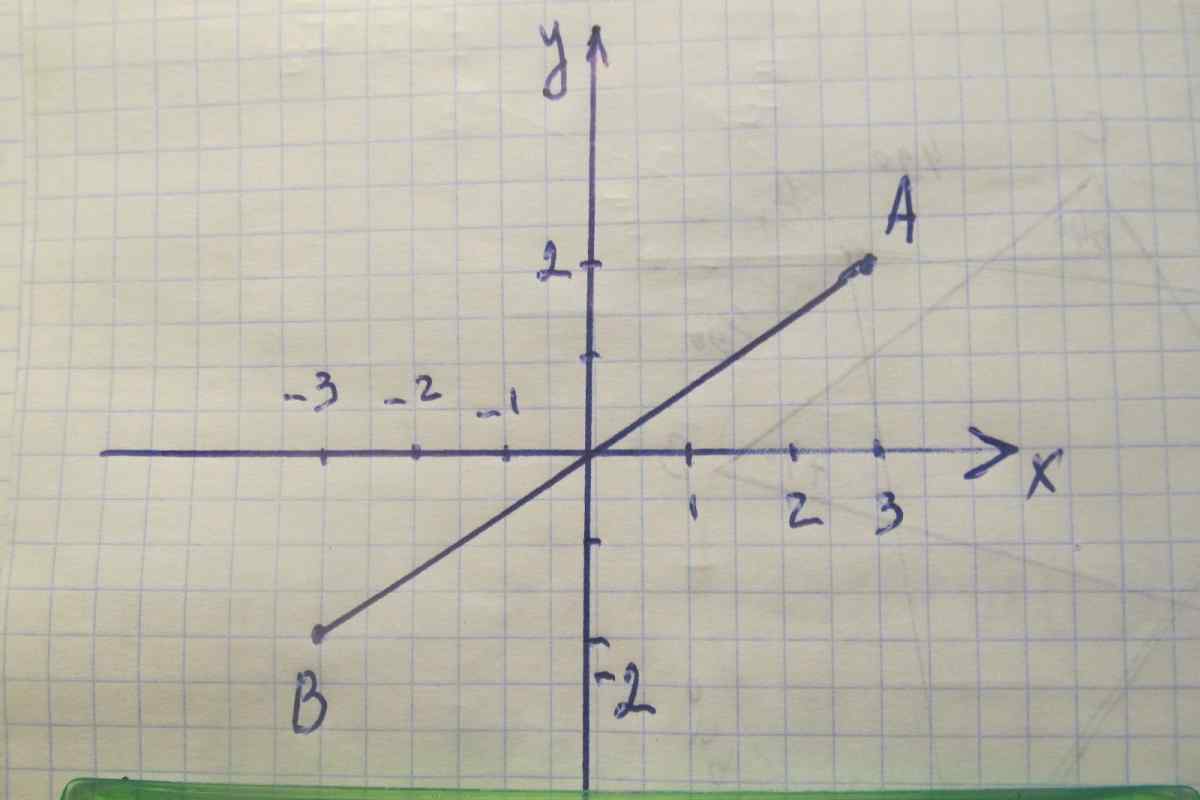
1. координати bвектора/b "" class = "" colorbox imagefield imagefield-imagelink "" rel = "" gallery-step-images "" > Помістіть на початок вектора, координати якого вам треба знайти, точку нульового відліку декартової системи координат. Після цього для визначення координати вектора знайдіть розташування кінцевої точки. Для цього опустіть по одному перпендикуляру на координатні осі Ікс і Ігрек. Таким чином, ви отримаєте точки, в яких вектор перетинається з осями. Визначте координати цих точок. Вони і будуть координатами вказаного вектора. Це стандартний спосіб визначення координат вектора на площині.
2. Якщо вам потрібно визначити координати вектора у просторі, будь ласка, дійте за таким же принципом, як і знаходження їх на площині. Це абсолютно такі ж спрямовані відрізки, які мають початок і кінець. Відмінність полягає лише в тому, що вектор у просторі задається не двома, а трьома координатами x, y і z (на площині це довжина і висота, а в просторі до всього додається ще й глибина) a (xa; ya; za), де а позначає довжину вектора. Таким чином, щоб знайти координати вектора в просторі, вам треба з координати кінця відняти координату початку вектора. Вирахуйте формулу: a =AB (xB − xA; yB − yA; zB − zA). Це лише один із способів вирішення завдань по стереометрії (вивчення фігур в просторі), в якому застосовуються прості формули, правила і алгоритми. Він займає мінімум часу і досить зручний.
3. Визначте координати вектора в просторі класичним способом, який вимагатиме від вас відмінного знання теорем і аксіом стереометрії, умінь будувати креслення і зводити об 'ємні завдання до метричних. Він хороший тим, що відмінно розвиває мозок і просторове мислення, але вимагає набагато більшого часу і при найменшій помилці дає невірні результати. Класичний спосіб зазвичай широко застосовується архітекторами при плануванні креслень майбутніх будівель.